51 Optimization
R provides a general purpose optimization tool, optim(). You can use it to estimate parameters that minimize any defined function.
Supervised and unsupervised learning involves defining a loss function to minimize or an objective function to minimize or maximize.
To learn how optim() works, let’s write a simple function that returns linear coefficients by minimizing squared error.
51.1 Data
51.2 GLM (glm, s_GLM)
Call:
glm(formula = y ~ x)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 11.979070 0.043252 276.962 <2e-16 ***
x1 0.061798 0.040916 1.510 0.1316
x2 -0.003873 0.043271 -0.090 0.9287
x3 1.488113 0.042476 35.034 <2e-16 ***
x4 0.031115 0.044015 0.707 0.4800
x5 0.034217 0.043664 0.784 0.4336
x6 0.034716 0.042189 0.823 0.4110
x7 3.183398 0.040605 78.399 <2e-16 ***
x8 -0.034252 0.043141 -0.794 0.4276
x9 0.541219 0.046550 11.627 <2e-16 ***
x10 0.087120 0.044000 1.980 0.0483 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for gaussian family taken to be 0.9207315)
Null deviance: 7339.42 on 499 degrees of freedom
Residual deviance: 450.24 on 489 degrees of freedom
AIC: 1390.5
Number of Fisher Scoring iterations: 2Or, using rtemis:
mod.glm <- s_GLM(x, y)10-03-24 19:02:10 Hello, egenn [s_GLM]
.:Regression Input Summary
Training features: 500 x 10
Training outcome: 500 x 1
Testing features: Not available
Testing outcome: Not available
10-03-24 19:02:11 Training GLM... [s_GLM]
.:GLM Regression Training Summary
MSE = 0.90
RMSE = 0.95
MAE = 0.77
r = 0.97 (p = 5.3e-304)
R sq = 0.94
10-03-24 19:02:11 Completed in 0.01 minutes (Real: 0.84; User: 0.37; System: 0.03) [s_GLM]
summary(mod.glm$mod)
Call:
glm(formula = .formula, family = family, data = df.train, weights = .weights,
na.action = na.action)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 11.979070 0.043252 276.962 <2e-16 ***
V1 0.061798 0.040916 1.510 0.1316
V2 -0.003873 0.043271 -0.090 0.9287
V3 1.488113 0.042476 35.034 <2e-16 ***
V4 0.031115 0.044015 0.707 0.4800
V5 0.034217 0.043664 0.784 0.4336
V6 0.034716 0.042189 0.823 0.4110
V7 3.183398 0.040605 78.399 <2e-16 ***
V8 -0.034252 0.043141 -0.794 0.4276
V9 0.541219 0.046550 11.627 <2e-16 ***
V10 0.087120 0.044000 1.980 0.0483 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for gaussian family taken to be 0.9207315)
Null deviance: 7339.42 on 499 degrees of freedom
Residual deviance: 450.24 on 489 degrees of freedom
AIC: 1390.5
Number of Fisher Scoring iterations: 2
51.3 optim()
Basic usage of optim to find values of parameters that minimize a function:
- Define a list of initial parameter values
- Define a loss function whose first argument is the above list of initial parameter values
- Pass parameter list and objective function to
optim
In the following example, we wrap these three steps in a function called linearcoeffs, which will output the linear coefficients that minimize squared error, given a matrix/data.frame of features x and an outcome y. We also specify the optimization method to be used (See ?base::optim for details):
linearcoeffs <- function(x, y, method = "BFGS") {
# 1. List of initial parameter values
params <- as.list(c(mean(y), rep(0, NCOL(x))))
names(params) <- c("Intercept", paste0("Coefficient", seq(NCOL(x))))
# 2. Loss function: first argument is parameter list
loss <- function(params, x, y) {
estimated <- c(params[[1]] + x %*% unlist(params[-1]))
mean((y - estimated)^2)
}
# 3. optim!
coeffs <- optim(params, loss, x = x, y = y, method = method)
# The values that minimize the loss function are stored in $par
coeffs$par
}coeffs.optim <- linearcoeffs(x, y)
estimated.optim <- cbind(1, x) %*% coeffs.optim
mplot3_fit(y, estimated.optim)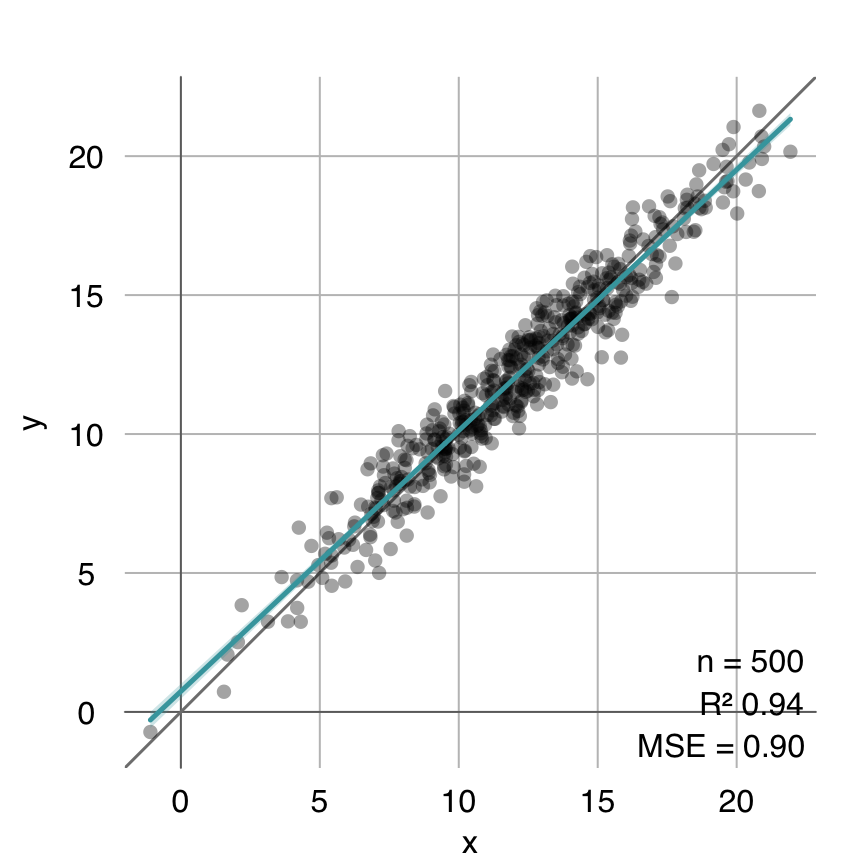
coeffs.glm <- mod.glm$mod$coefficients
estimated.glm <- cbind(1, x) %*% coeffs.glm
mplot3_fit(y, estimated.glm)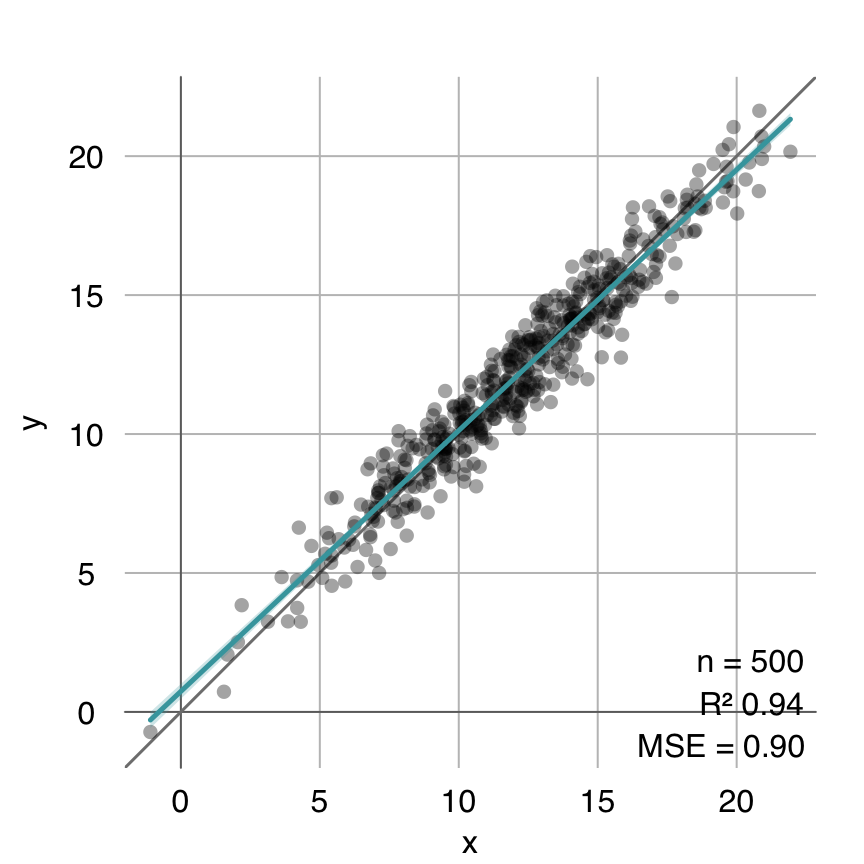
mplot3_fit(coeffs.glm, coeffs.optim)